Donde:
- f(x,y) es la imagen de entrada.
- g(x,y) es la imagen procesada.
- T es un operador en f definida sobre alguna vecindad. La vecindad donde se aplica el operador T generalmente es un rectangulo, matriz de n*n.
- Si la vecindad es de 1x1 entonces es una operación puntual y la función de transformación tomará la forma :
Donde s y r son variables que denotan niveles de grises para f(x,y) y g(x,y) respectivamente.
Funciones básicas de transformaciones en escala de grises usadas para el mejoramiento de imágenes
- Funciones lineales (Negativo e identidad).
- Funciones logarítmicas (logaritmo y logaritmo invertido).
- Funciones potencia (n-potencia y n-raiz).
- Funciones de transformación lineales por trozos.
- Funciones Lineales:(Negativo)
- El negativo de una imagen con un rango de nivel de grises entre [0 , L - 1], está dado por la expresión:
s = L - 1 - r
- Esta función invierte los niveles de intensidad de esta manera se produce el equivalente de un negativo fotografico. Este tipo de procesamiento es útil para mejarar niveles de blancos o grises en regiones oscuras de la imagen, especialmente cuando las areas negras dominan en tamaño.
- Prueba:

- Funciones Logarítmicas: La forma general de esta transformación es:
- Donde c esuna constante y se asume que r es mayor o igual que 0 a la quinta. El efecto de esta transformación es mapear un pequeño rango de valores bajos de nivel de gris a un rango más amplio de niveles de salida, al tiempo que lo contrario ocurre con los valores de entrada altos.
- Se usa una transformación de este tipo para expander los valores de píxeles oscuros de una imagen, mientras se comprime los valores de alto valor. La transformación logarítmica inversa lleva a cabo la transformación contraria.

- Prueba donde c=2:

- Funciones de Potencia: Su forma general es:
- Donde c y a son constantes positivas. Algunas veces la ecuación se escribe como s = c* (r + e)ª para tomar en cuenta un offset de calibración. Al variar la variable a obtenemos las diversas transformaciones que se grafican a continuación.

- Como en el caso de la transformacion logarítmica, las curvas de función de potencia con valores fraccionales de a mapean un rango pequeño de valores oscuros en un rango amplio de valores de salida y lo contrario con los valores claros de entrada. Esta tranformación es usada para manipular el contraste de la imagen.
- Recorte de plano de bits:

- Para algunas aplicaciones, es deseable conocer la contribución de cada bit específico en la apariencia total de la imagen.
- Supóngase que cada pixel de una imagen es representado por 8 bits. Imigínese que la imagen se compone de 8 planos de 1 bit, desde el plano de 0 bits (el bit menos significativo) hasta el plano de bits 7 (más significativo). El plano de bits contiene todos los LSB de cada byte de cada pixel en la imagen y el plano 7 contiene los MSB de cada byte de cada pixel de la imagen.
- Con esto obtenemos 7 imágenes binarias (una por cada plano). Este proceso ayuda a determinar la cantidad de bits necesaria para cuantificar una imagen, tambien es util para la compresión de imagenes.
- Prueba: Donde el plano es igual a 7, 5, 0 respectivamente:



Procesamiento del Histograma:
El histograma es una imagen digital con niveles de gris en el rango [0, L-1] de una función discreta:

Donde rk es el nivel de grises k-esimo y nk es el número de píxeles en la imagen con niveles de grises rk.
Los histogramas son la base de muchas técnicas de procesamiento de la imagen en el dominio espacial.
- Histograma Normalizado: Para normalizar el histograma se divide cada uno de sus valores entre el número total de píxeles en la imagen, n. Asi el histograma normalizado se obtiene de:

- Para k = 1, 2, 3, ..., L-1.
- Ecualización del Histograma: La ecualizacion nos permitirá que la imagen eleve su contraste y exhiba una gran variedad de tonos de gris. Para la ecualización trabajaremos con el caso discreto:

- Donde n es el número total de píxeles en la imagen, nk es el número de píxeles que tienen nivel de gris rk, y L es el número total de posibles niveles de gris de la imagen.
- Prueba:

- Ecualización Uniforme: El histograma se modifica de tal forma que la imagen resultante de los niveles de gris se representa de forma equitativa en todo el rango de valores establecido. Esta ecualización tiene la siguiente expresión:

- Donde: rmin es el valor minimo de intensidad de pixel que contiene la imagen de entrada y rmax es el valor máximode intensidad de pixel que contiene la imagen de entrada.
- Prueba:

- Ecualización Exponencial: Esta ecualización nos permite distribuir el histograma según una función exponencial. Esta ecualización tiene la siguiente expresión:
Donde: rmin es el valor minimo de intensidad de pixel que contiene la imagen de entrada.
- Prueba donde alpha=0.01:

- Ecualización Rayleigh: Se trata de distribuir el histograma según la siguiente expresión:

- Donde: rmin es el valor minimo de intensidad de pixel que contiene la imagen de entrada.
- Prueba donde alpha=50:

- Ecualización Hipercúbica: Se trata de distribuir el histograma según la siguiente expresión:

- Donde: rmin es el valor minimo de intensidad de pixel que contiene la imagen de entrada y rmax es el valor máximode intensidad de pixel que contiene la imagen de entrada.

- Ecualización Logaritmo Hiperbólica: Se trata de distribuir el histograma según la siguiente expresión:

- Donde: rmin es el valor minimo de intensidad de pixel que contiene la imagen de entrada y rmax es el valor máximode intensidad de pixel que contiene la imagen de entrada.
- Prueba:

Expansión del Histograma: La función para expandir el histograma se define como:
Donde f(x,y) es el nivel de gris de la imagen de entrada, g(x,y) es el nivel de gris de la imagen de salida, f(i,j)max es el mayor valor del nivel de gris en la imagen de entrada f, f(i,j)min es el menor valor del nivel de gris de la imagen de entrada f, MAX y MIN corresponden al máximo y al mínimo valores posibles de los niveles de gris(para una imagen codificada con 8 bits sería 0 y 255).
- Pruba donde MIN=0 y MAX=255:

Contracción del Histograma: La funcion para contraer el histograma se define como:
- Prueba: donde Cmin=100 y Cmax=250:

Donde rk es el nivel de gris de la imagen de entrada, sk es el nivel de gris de la imagen de salida, DES es el valor de desplazamiento.
- Prueba: donde DES=50:

Donde:
Se pretende:
La idea general es encontrar los valores zk correspondientes a sk que satisfagan la ecuación sk=zk.
Esta ecuación se da pues trabajamos con enteros.
- Pruebas:



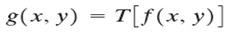










No hay comentarios:
Publicar un comentario